The post is also available as pdf.
Cayley-Hamilton theorem is usually presented in a linear algebra context, which says that an 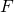 -vector space endomorphism (and its matrix representation) satisfies its own characteristic polynomial. Actually, this result can be generalised a little bit to all modules over commutative rings (which are certainly required to be finitely generated for determinant to make sense). There are many proofs available, among which is the bogus proof of substituting the matrix into the characteristic polynomial
-vector space endomorphism (and its matrix representation) satisfies its own characteristic polynomial. Actually, this result can be generalised a little bit to all modules over commutative rings (which are certainly required to be finitely generated for determinant to make sense). There are many proofs available, among which is the bogus proof of substituting the matrix into the characteristic polynomial 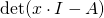 and obtaining
and obtaining
![Rendered by QuickLaTeX.com \[ \det (A \cdot I - A) = \det (A - A) = 0. \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-ee6f8d60f14590e9041eee70f70d8050_l3.png)
The reason it doesn’t work is because the product 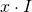 in the characteristic polynomial is multiplication of a matrix by a scalar, while the product assumed in the bogus proof is matrix multiplication. In this post I will show that the intuition behind this “substitution-and-cancellation” is correct (in a narrow sense), and the proof is rescuable by using a trick, which in itself is quite useful.
in the characteristic polynomial is multiplication of a matrix by a scalar, while the product assumed in the bogus proof is matrix multiplication. In this post I will show that the intuition behind this “substitution-and-cancellation” is correct (in a narrow sense), and the proof is rescuable by using a trick, which in itself is quite useful.
I will develop the theory using language of rings and modules but if you don’t understand that, feel free to substitute “fields” and “vector spaces” in place.
Let 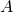 be a commutative ring and
be a commutative ring and 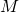 be an
be an 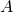 -module generated by
-module generated by 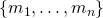 . Note that
. Note that 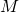 is naturally an
is naturally an 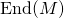 -module and for all
-module and for all 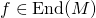 , write
, write ![Rendered by QuickLaTeX.com [f] \in \matrixring_n(A)](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-df5376d152e40098656afd8d07ecd02d_l3.png) for its representation with respect to the generators above, i.e.
for its representation with respect to the generators above, i.e. ![Rendered by QuickLaTeX.com f(m_i) = \sum_j [f]_{ij}m_j](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-c7f9826df4edf106e9d4a9bc4a38bb5e_l3.png) . In particular, there is a ring homomorphism
. In particular, there is a ring homomorphism 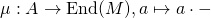 sending an element to its multiplication action. Let
sending an element to its multiplication action. Let 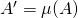 .
.
There is a technical remark to make: later we will use determinant of matrices over 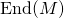 , which is non-commutative. However, throughout the discussion we are concerned with only one endomorphism
, which is non-commutative. However, throughout the discussion we are concerned with only one endomorphism 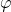 (besides multiplication, of course) so we can restrict the scalars to
(besides multiplication, of course) so we can restrict the scalars to ![Rendered by QuickLaTeX.com A'[\varphi]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-8fa83b946927d2481a05046fb7176c03_l3.png) , a subring contained in the centre of
, a subring contained in the centre of 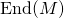 .
.
Given a module endomorphism 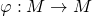 , its characteristic polynomial is defined to be
, its characteristic polynomial is defined to be
![Rendered by QuickLaTeX.com \[ \chi_{[\varphi]}(x) = \det (x \cdot I - [\varphi]) \in A[x] \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-896202a3916dde864a1d81678aebf78f_l3.png)
where 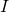 is the
is the 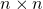 identity matrix and the product
identity matrix and the product 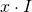 is multiplication of a matrix by a scalar. Note that
is multiplication of a matrix by a scalar. Note that 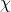 is generator dependent in general. We have
is generator dependent in general. We have
Cayley-Hamilton Theorem
![Rendered by QuickLaTeX.com \[ \chi_{[\varphi]}(\varphi) = 0. \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-604181981cf7977f6c4a57d3b5c4767e_l3.png)
Note that this is a relation of endomorphisms with coefficients in 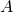 .
.
Proof: Let ![Rendered by QuickLaTeX.com [\varphi]_{ij} = a_{ij}](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-691ae36dcaf777360039a04760498c08_l3.png) and view
and view 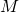 as an
as an ![Rendered by QuickLaTeX.com A'[\varphi]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-8fa83b946927d2481a05046fb7176c03_l3.png) -module. Since
-module. Since
![Rendered by QuickLaTeX.com \[ \varphi m_i = \sum_j a_{ij}m_j, \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-6ab8dccea5d97fb00d42c03625feae98_l3.png)
we have
(*) 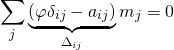
with
![Rendered by QuickLaTeX.com \[ \Delta = \varphi \cdot I - N \in \matrixring_n(A'[\varphi]). \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-ce51a29e77b256fb8a6fa0bc086fe1ba_l3.png)
Again, the multiplication is by scalar 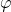 , viewed as an element of the ring
, viewed as an element of the ring 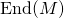 .
.
Claim that if ![Rendered by QuickLaTeX.com \det \Delta = 0 \in A'[\varphi]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-860eaaa797b5bc3714c5c715ddbe3061_l3.png) then we are done: consider the ring homomorphism
then we are done: consider the ring homomorphism
![Rendered by QuickLaTeX.com \begin{align*} A[x] &\to \End(M) \\ x &\mapsto \varphi \end{align*}](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-f26a8f7a60dc88ecd3d2459f1e04438e_l3.png)
which maps ![Rendered by QuickLaTeX.com \chi_{[\varphi]}(t) \mapsto \chi_{[\varphi]}(\varphi) = \det \Delta](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-1db550819808c672dfe241aa0c50d216_l3.png) since
since 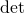 is a polynomial function. So done.
is a polynomial function. So done.
To show this, recall that
![Rendered by QuickLaTeX.com \[ (\adj \Delta) \cdot \Delta = \det \Delta \cdot I \in \matrixring_n(A'[\varphi]) \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-d0a64fdb3d6d78b73a3c090e41ce0b61_l3.png)
where multiplication on the left is between matrices. Let 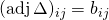 . Then multiply
. Then multiply 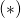 by
by 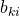 and apply the identity,
and apply the identity,
![Rendered by QuickLaTeX.com \[ \sum_{i, j} (b_{ki} \Delta_{ij}) m_j = \sum_j (\det \Delta \delta_{kj}) m_j = (\det \Delta) m_k = 0. \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-00d27817d71c92cc4a92c54f1a1d8d66_l3.png)
so 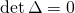 as required.
as required.
If you feel that little work is done in the proof and suspect it might be tautological somewhere (which I had when I first saw this proof), go through it again and convince yourself it is indeed a bona fide proof. There are two tricks used here: firstly we extend the scalars by recognising 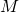 as an
as an ![Rendered by QuickLaTeX.com A'[\varphi]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-8fa83b946927d2481a05046fb7176c03_l3.png) ring so that action by
ring so that action by 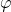 becomes multiplication. This is essentially since it allows us to treat
becomes multiplication. This is essentially since it allows us to treat 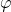 and scalar multiplication by
and scalar multiplication by 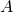 on an equal footing. Secondly, the ring homomorphism
on an equal footing. Secondly, the ring homomorphism ![Rendered by QuickLaTeX.com A[x] \to A'[\varphi]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-25e41df3e08bd7843e0540edfd727441_l3.png) substitutes
substitutes 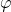 in place of
in place of 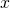 . Aha, the intuition in the bogus proof is correct, but we need a little extra work to sort out the notation to express precisely what we mean.
. Aha, the intuition in the bogus proof is correct, but we need a little extra work to sort out the notation to express precisely what we mean.
The key idea in the proof, sometimes called the determinant trick, has many applications in commutative algebra:
Let 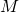 be an
be an 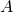 -module generated by
-module generated by 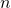 elements and
elements and 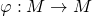 a homomorphism. Suppose
a homomorphism. Suppose 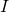 is an ideal of
is an ideal of 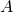 such that
such that 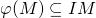 , then there is a relation
, then there is a relation
![Rendered by QuickLaTeX.com \[ \varphi^n + a_1 \varphi^{n - 1} + \dots + a_{n - 1} \varphi + a_n = 0 \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-5892cc385c0f79dfeee5e111eecb785d_l3.png)
where 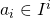 for all
for all 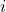 .
.
Proof: Let 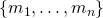 be a set of generators of
be a set of generators of 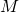 . Since
. Since 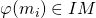 , we can write
, we can write
![Rendered by QuickLaTeX.com \[ \varphi m_i = \sum_j a_{ij}m_j \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-2c7595143b2f66f50cf8b33fba7ad03b_l3.png)
with 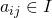 . Multiply
. Multiply
![Rendered by QuickLaTeX.com \[ \sum_j \underbrace{(\varphi \delta_{ij} - a_{ij})}_{\Delta_{ij}} m_j = 0 \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-09c6f02aa9dde4c52a44f8fd13715d42_l3.png)
by 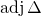 , we deduce that
, we deduce that 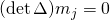 so
so 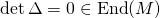 . Expand.
. Expand.
An immediate corollary is Nakayama’s Lemma, which alone is an important result in commutative algebra:
Nakayama’s Lemma
If 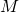 is a finitely generated
is a finitely generated 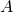 -module and
-module and 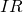 is such that
is such that 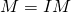 then there exists
then there exists 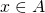 such that
such that 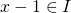 and
and 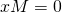 .
.
Proof: Apply the trick to 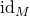 . Since
. Since 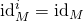 and
and 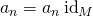 , we get
, we get
![Rendered by QuickLaTeX.com \[ \left(1 + \sum_{i = 1}^n a_i\right) \id_M = 0. \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-3349c2fe8b8bcedb371b9edd18a12400_l3.png)
We use the result to prove a rather interesting fact about module homomorphism:
Let 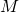 be a finitely generated
be a finitely generated 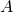 -module. Then every surjective module homomorphism on
-module. Then every surjective module homomorphism on 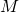 is also injective.
is also injective.
Proof: Let 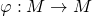 be surjective. Let
be surjective. Let 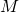 be an
be an ![Rendered by QuickLaTeX.com A'[\varphi]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-8fa83b946927d2481a05046fb7176c03_l3.png) module and
module and ![Rendered by QuickLaTeX.com I = (\varphi) \ideal A'[\varphi]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-cab6c1b312d8200a3e0e0d51c774b673_l3.png) . Then
. Then 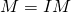 by surjectivity of
by surjectivity of 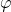 . Thus by Nakayama’s Lemma, there exists
. Thus by Nakayama’s Lemma, there exists 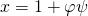 ,
, ![Rendered by QuickLaTeX.com \psi \in A'[\varphi]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-163b98a08ed9d15bdf4b94f3a8f668ab_l3.png) such that
such that 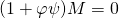 , i.e. for all
, i.e. for all 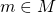 ,
, 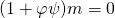 . It follows that
. It follows that 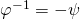 .
.
As a side note, the converse is not true: injective module homomorphisms need not be surjective. For example 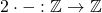 .
.
References
M. Reid, Undergraduate Commutative Algebra, §2.6 – 2.8
![]() is an open interval, one can reasonably consider the following rings of functions on
is an open interval, one can reasonably consider the following rings of functions on ![]() :
: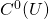 : all continuous functions
: all continuous functions 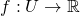 ;
;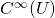 : all smooth functions (that is, differentiable to any order);
: all smooth functions (that is, differentiable to any order);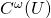 : all analytic functions (that is, convergent power series);
: all analytic functions (that is, convergent power series);![Rendered by QuickLaTeX.com \mathbb R[X]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-fb651f85d961081ac3038655a3276bdc_l3.png) : the polynomial ring, viewed as a polynomial function on
: the polynomial ring, viewed as a polynomial function on 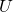 .
.![]() .
.![]() to the topological category,
to the topological category, ![]() to the differentiable category (differentiable manifolds),
to the differentiable category (differentiable manifolds), ![]() to real analytic geometry, and
to real analytic geometry, and ![]() to algebraic geometry.
to algebraic geometry.![]() will reveal that the differentiable functions have measure
will reveal that the differentiable functions have measure ![]() in the continuous functions. The gap between
in the continuous functions. The gap between ![]() and
and ![]() is exemplified by the behaviour of
is exemplified by the behaviour of ![]() , the standard function which is differentiable infinitely often, but for which the Taylor series (at
, the standard function which is differentiable infinitely often, but for which the Taylor series (at ![]() ) does not converge to the function. Using this one can easily build a bump function that is
) does not converge to the function. Using this one can easily build a bump function that is ![]() on a compact set and vanishes outside any given open set containing the compact set. In contrast, an analytic function on
on a compact set and vanishes outside any given open set containing the compact set. In contrast, an analytic function on ![]() extends (as a convergent power series) to an analytic function of a complex variable on a suitable domain in
extends (as a convergent power series) to an analytic function of a complex variable on a suitable domain in ![]() , so that (using results from complex analysis) if
, so that (using results from complex analysis) if ![]() vanishes on a real interval, it must vanish identically. This is a kind of “rigid” property which characterises analytic geometry as opposed to differential topology.
vanishes on a real interval, it must vanish identically. This is a kind of “rigid” property which characterises analytic geometry as opposed to differential topology.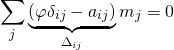
![Rendered by QuickLaTeX.com \[ \sum_j \underbrace{(\varphi \delta_{ij} - a_{ij})}_{\Delta_{ij}} m_j = 0 \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-09c6f02aa9dde4c52a44f8fd13715d42_l3.png)
![Rendered by QuickLaTeX.com \[ \left(1 + \sum_{i = 1}^n a_i\right) \id_M = 0. \]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-3349c2fe8b8bcedb371b9edd18a12400_l3.png)