This post is almost verbatim from Undergraduate Algebraic Geometry § 0.3.
The specific flavour of algebraic geometry comes from the use of only polynomial functions (together with rational functions); to explain this, if ![]() is an open interval, one can reasonably consider the following rings of functions on
is an open interval, one can reasonably consider the following rings of functions on ![]() :
:
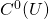 : all continuous functions
: all continuous functions 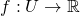 ;
;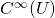 : all smooth functions (that is, differentiable to any order);
: all smooth functions (that is, differentiable to any order);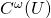 : all analytic functions (that is, convergent power series);
: all analytic functions (that is, convergent power series);![Rendered by QuickLaTeX.com \mathbb R[X]](http://qk206.user.srcf.net/wp-content/ql-cache/quicklatex.com-fb651f85d961081ac3038655a3276bdc_l3.png) : the polynomial ring, viewed as a polynomial function on
: the polynomial ring, viewed as a polynomial function on 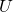 .
.
There are of course inclusions ![]() .
.
These rings of functions correspond to some of the important categories of geometry: ![]() to the topological category,
to the topological category, ![]() to the differentiable category (differentiable manifolds),
to the differentiable category (differentiable manifolds), ![]() to real analytic geometry, and
to real analytic geometry, and ![]() to algebraic geometry.
to algebraic geometry.
The point I want to make here is that each of these inclusion signs represents an absolutely huge gap, and that this leads to the main characteristics of geometry in the different categories. Although it’s not stressed very much in school and first year university calculus, any reasonable way of measuring ![]() will reveal that the differentiable functions have measure
will reveal that the differentiable functions have measure ![]() in the continuous functions. The gap between
in the continuous functions. The gap between ![]() and
and ![]() is exemplified by the behaviour of
is exemplified by the behaviour of ![]() , the standard function which is differentiable infinitely often, but for which the Taylor series (at
, the standard function which is differentiable infinitely often, but for which the Taylor series (at ![]() ) does not converge to the function. Using this one can easily build a bump function that is
) does not converge to the function. Using this one can easily build a bump function that is ![]() on a compact set and vanishes outside any given open set containing the compact set. In contrast, an analytic function on
on a compact set and vanishes outside any given open set containing the compact set. In contrast, an analytic function on ![]() extends (as a convergent power series) to an analytic function of a complex variable on a suitable domain in
extends (as a convergent power series) to an analytic function of a complex variable on a suitable domain in ![]() , so that (using results from complex analysis) if
, so that (using results from complex analysis) if ![]() vanishes on a real interval, it must vanish identically. This is a kind of “rigid” property which characterises analytic geometry as opposed to differential topology.
vanishes on a real interval, it must vanish identically. This is a kind of “rigid” property which characterises analytic geometry as opposed to differential topology.
References
M. Reid, Undergraduate Algebraic Geometry, § 0.3